LISTRIK STATIS Muatan listrik,
Q, adalah muatan dasar yang dimiliki suatu benda. Satuan Q adalah
coulomb, yang merupakan 6.24 x 10
18 muatan dasar.
Q adalah sifat dasar yang dimiliki oleh materi baik itu berupa proton (muatan positif) maupun elektron (muatan negatif). Muatan listrik total suatu atom atau materi ini bisa positif, jika atomnya kekurangan elektron. Sementara atom yang kelebihan elektron akan bermuatan negatif. Besarnya muatan tergantung dari kelebihan atau kekurangan elektron ini, oleh karena itu muatan materi/atom merupakan kelipatan dari satuan Q dasar. Dalam atom yang netral, jumlah proton akan sama dengan jumlah elektron yang mengelilinginya (membentuk muatan total yang netral atau tak bermuatan).
Hukum Coulomb adalah hukum yang menjelaskan hubungan antara gaya yang timbul antara duatitik muatan, yang terpisahkan jarak tertentu, dengan nilai muatan dan jarak pisah keduanya.
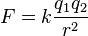
Hukum ini menyatakan apabila terdapat dua buah titik muatan maka akan timbul gaya di antara keduanya, yang besarnya sebanding dengan perkalian nilai kedua muatan dan berbanding terbalik dengan kuadrat jarak antar keduanya . Interaksi antara benda-benda bermuatan (tidak hanya titik muatan) terjadi melaluigaya tak kontak yang bekerja melampaui jarak separasi . Adapun hal lain yang perlu diperhatikan adalah bahwa arah gaya pada masing-masing muatan terletak selalu sepanjang garis yang menghubungkan kedua muatan tersebut . Gaya yang timbul dapat membuat kedua titik muatan saling tarik-menarik atau saling tolak-menolak, tergantung nilai dari masing-masing muatan. Muatan sejenis (bertanda sama) akan saling tolak-menolak, sedangkan muatan berbeda jenis akan saling tarik-menarik .
Notasi vektor
Dalam notasi vektor, hukum Coloumb dapat dituliskan sebagai

yang dibaca sebagai gaya yang dialami oleh muatan
q1 akibat adanya muatan
q2. Untuk gaya yang dialami oleh muatan
q2 akibat adanya muatan
q1 dituliskan dengan menukarkan indeks

, atau melalui hukum ketiga Newton dapat dituliskan

Medan adalah suatu besaran yang mempunyai harga pada tiap titik dalam ruang. Atau secara matematis, medan merupakan sesuatu yang merupakan fungsi kontinu dari posisi dalam ruang. Medan ada dua macam yaitu :
- Medan Skalar, misalnya temperatur, potensial dan ketinggian
- Medan vektor, misalnya medan listrik dan medan magnet Untuk membahas suatu medan listrik, digunakan pengertian kuat medan, yakni : “Vektor gaya Coulomb yang bekerja pada suatu muatan yang kita lewatkan pada suatu titik dalam medan gaya ini”, dan dinyatakan sebagai E(r). dalam bentuk matematis :
 Dengan menggunakan persamaan harus diingat ; - hubungan ini hanya berlaku untuk muatan sumber berupa titik
- pusat sistem koordinat ada pada muatan sumber - besaran yang digunakan dalam sistem MKS
- hubungan diatas hanya berlaku dalam vakum atau udara X.2.1 Kuat Medan Listrik oleh Satu Muatan Titik
Muatan sumber q berupa muatan titik terletak pada vektor posisi r’, sedang titi p pada posisi r. Posisi relatif p terhadap muatan sumber adalah (r-r’), vektor satuan arah SP adalah
Dengan menggunakan persamaan harus diingat ; - hubungan ini hanya berlaku untuk muatan sumber berupa titik
- pusat sistem koordinat ada pada muatan sumber - besaran yang digunakan dalam sistem MKS
- hubungan diatas hanya berlaku dalam vakum atau udara X.2.1 Kuat Medan Listrik oleh Satu Muatan Titik
Muatan sumber q berupa muatan titik terletak pada vektor posisi r’, sedang titi p pada posisi r. Posisi relatif p terhadap muatan sumber adalah (r-r’), vektor satuan arah SP adalah
 Jadi kuat medan listrik E di titik r oleh muatan q adalah
Jadi kuat medan listrik E di titik r oleh muatan q adalah  X.2.2 Kuat Medan Listrik oleh Beberapa Muatan Titik Jika sumber muatan berupa beberapa muatan titik yang berbeda besar dan posisinya, maka kuat medan listrik resultan E (r )adalah penjumlahan masing-masing kuat medan, dimana secara matematis dinyatakan sebagai
X.2.2 Kuat Medan Listrik oleh Beberapa Muatan Titik Jika sumber muatan berupa beberapa muatan titik yang berbeda besar dan posisinya, maka kuat medan listrik resultan E (r )adalah penjumlahan masing-masing kuat medan, dimana secara matematis dinyatakan sebagai
 Bila ada N buah muatan titik sebagai sumber, dengan muatan sumber q1 yang masing-masing berada pada jarak ri’, maka medan resultan pada vector posisi r adalah :
Bila ada N buah muatan titik sebagai sumber, dengan muatan sumber q1 yang masing-masing berada pada jarak ri’, maka medan resultan pada vector posisi r adalah :  Contoh 3 Dua buah muatan berada pada bidang x-y dengan masing-masing muatan q1 = 7
Contoh 3 Dua buah muatan berada pada bidang x-y dengan masing-masing muatan q1 = 7 C pada pusat koordinat dan muatan q2 = 5
C pada pusat koordinat dan muatan q2 = 5  C terletak pada sumbu x positif berjarak 0,3 meter dari pusat koordinat.
a. tentukan besar dan arah kuat medan listrik di titik P yang terletak pada sumbu y positif yang berjarak 0,4 meter dari pusat koordinat.
b. Tentukan gaya yang dialami oleh muatan sebesar 2 x 10-3 C jika terletak di titik P. Penyelesaian :
C terletak pada sumbu x positif berjarak 0,3 meter dari pusat koordinat.
a. tentukan besar dan arah kuat medan listrik di titik P yang terletak pada sumbu y positif yang berjarak 0,4 meter dari pusat koordinat.
b. Tentukan gaya yang dialami oleh muatan sebesar 2 x 10-3 C jika terletak di titik P. Penyelesaian :

Michael Faraday memperkenalkan cara menggambarkan medan (listrik, magnet, maupun gravitasi) melalui konsep garis gaya (garis medan). Garis gaya adalah garis-garis lengkung dalam medan yang dapat menunjukkan arah serta besarnya E pada setiap titik masing-masing dengan garis singgung dan kerapatan garisnya pada titik yang bersangkutan

Garis-garis gaya berawal pada titik muatan positif dan berakhir pada titik muatan negatif. Diantara titik awal dan titik akhir, garis gaya selalu kontinu dan tidak mungkin berpotongan, kecuali pada titik muatan lain yang terdapat diantaranya

Jumlah garis-garis gaya listrik yang menembus suatu permukaan secara tegak lurus didefenisikan sebagai fluks magnetic

. Bila diketahui kuat medan E, maka jumlah garis gaya d

yang menembus suatu elemen dA tegak lurus pada E adalah :

Bila permukaan dA tidak tegak lurus maka jumlah garis yang keluar dari dA haruslah

Dimana dA = ndA atau n adalah vektor normal dan

sudut antara dA dengan bidang yang tegak lurus pada E. Bila kuat medan pada elemen seluas dA dan E, maka jumlah garis gaya yang keluar dari seluruh permukaan S adalah :

Elemen luas dA berada pada permukaan S harga medan ;listrik E diambil semua titik pada permukaan S.

Fluks listrik total untuk seluruh permukaan

Tanda menyatakan integrasi yang meliputi seluruh permukaan A. Untuk permukaan tertutup, elemen dA tegak lurus permukaan dan arahnya keluar. Fluks total untuk permukaan tertutup

Ternyata ada hubungan yang erat antara fluks listrik pada suatu permukaan tertutup dengan muatan listrik yang berada dalam permukaan tersebut dan hubungan ini dikenal dengan hukum Gauss, yaitu”jumlah garis gaya yang keluar dari suatu permukaan tertutup sebanding dengan jumlah muatan listrik yang dilingkupi oleh permukaan tetutup tersebut. Secara matematis

Dimana S adalah suatu permukaan tertutup

q
i adalah jumlah muatan yang ada di dalam atau dilingkupi oleh permukaan tetutup S. jadi dengan hukum gauss kita dapat menentukan muatan yang ada di dalam permukaan tetutup, bila kita tahu berapa garis gaya yang keluar dari permukaan tetutup tersebut. Contoh 4.

Di dalam ruang seperti pada gambar di atas terdapat medan listrik serba sama sebesar 10N/C berarah sumbu z kebawah. Hitung jumlah garis gaya yang keluar dari a. Luas OABC (luas OABC = 2 m
2)
b. Luas OFDC (luas OFDC = 2 m
2) Penyelesaian
a. Kuat medan listrik secara vector adalah E = -k 10 N/C Banyaknya garis gaya

Atau garis gaya banyaknya 20 buah dan arahnya menembus bidang OABC. Arah dA ada pada sumbu z positif sehingga d = dA
b. pada bidang ini dA = -jdA sehingga

Pada mekanika telah diuraikan hukum kkekalan energi mekanik Total, EK + EP konstan, yang sangat berguna untuk penyelesaian soal-soal. Hukum tersebut berlaku dalam medan gaya konservatif seperti medan gaya gravitasi. Berhubung medan medan gaya coulomb dengan bentuk pernyataannya yang sama dengan medan gravitasi, sewajarnya kita mengharapkan sifat yang serup pula dari medan gaya coulomb (medan elektrostatik) tersebut. Memang dapat ditunjukkan bahwa medan elektrostatik adalah bersifat konservatif sehingga dapat pula kita defenisikan disini energi potensial listrik, dan berlaku pula hubungan EK + EP = Konstan. Dalam mekanika telah ditunjukkan bahwa gaya gravitasi bersifat konservatif, yaitu kerja yang dilakukan medan gaya tidak bergantung kepada lintasannya. Jika suatu muatan q’ diletakkan dalam medan listrik, gaya listrik q’ adalah q’. Gaya ini adalah jumlah vektor dari gaya-gaya yang bekerja pada q’ oleh berbagai muatan yang menghasilkan kuat medan.Masing-masing gaya memenuhi Hukum Coulomb bersifat konservatif sehingga gaya q’ juga bersifat konservatif.
Kerja yang dilakukan oleh gaya listrik q’E pada muatan uji q’ untuk perpindahanyang sangat kecil ds adalah

Menurut defenisi, kerja yang dilakukan oleh gaya konservatif adalah negatif dari perubahan energi potensial(dU), sehingga:

Untuk suatu perpindahan muatan uji dari titik A ke B, potensialnya adalah:

dengan dU=beda energi yang dihasilkan UB=energi potensial pada posisi B (kedudukan akhir) UA = energi potensial pada posisi A(kedudukan awal) Misalkan ada (+q) di titik 0 dan muatan uji q’ di titik Q, gaya yang bekerja pada muatan uji adalah :

Untuk mencari beda energi potensial bila muatan q’ dipindahkan dari Q ke P adalah sebagai berikut :

atau secara umum, energi potensial medan listrik dari muatan (q) oleh muatan uji (q’) pada jarak r adalah :

Dalam membahas medan listrik , kita tidak menggunakan pengertian energi potensial tetapi menggunakan pengertian potensial listrik yaitu potensial persatuan muatan. Muatan listrik biasanya dituliskan sebagai :

Dan mempunyai satuan volt atau joule/coulomb. Beda potensial listrik juga dapat dituliskan dalam bentuk lain, yaitu :

atau dimana Dari dua persamaan di atas, maka dapat dilihat bahwa potensial listrik juga suatu medan listrik. Tetapi potensial listrik merupakan interaksi medan skalar dengan gaya Coulomb. Sekarang bagaimana menentukan potensial listrik bila diketahui medan listrik E(r). Untuk menghitung E( r ) dan V( r ) harus melakukan operasi diferensial. Oleh karena kuat medan adalah besaran vektor, operator diferensial harus operasi vektor, operasi ini disebut gradien yang dinyatakan sebagai ?. Sehingga kuat medan E( r ) dapat ditulis sebagai :

Dimana dapat dinyatakan dalam berbagai koordinat : Kartesian

Kapasitor adalah komponen elektronika yang dapat menyimpan muatan listrik. Struktur sebuah kapasitor terbuat dari 2 buah plat metal yang dipisahkan oleh suatu bahan dielektrik. Bahan-bahan dielektrik yang umum dikenal misalnya udara vakum, keramik, gelas dan lain-lain. Jika kedua ujung plat metal diberi tegangan listrik, maka muatan-muatan positif akan mengumpul pada salah satu kaki (elektroda) metalnya dan pada saat yang sama muatan-muatan negatif terkumpul pada ujung metal yang satu lagi. Muatan positif tidak dapat mengalir menuju ujung kutup negatif dan sebaliknya muatan negatif tidak bisa menuju ke ujung kutup positif, karena terpisah oleh bahan dielektrik yang non-konduktif. Muatan elektrik ini "tersimpan" selama tidak ada konduksi pada ujung-ujung kakinya. Di alam bebas, phenomena kapasitor ini terjadi pada saat terkumpulnya muatan-muatan positif dan negatif di awan.

Gambar 1 : prinsip dasar kapasitor
Kapasitansi
Kapasitansi didefenisikan sebagai kemampuan dari suatu kapasitor untuk dapat menampung muatan elektron. Coulombs pada abad 18 menghitung bahwa 1 coulomb = 6.25 x 1018 elektron. Kemudian Michael Faraday membuat postulat bahwa sebuah kapasitor akan memiliki kapasitansi sebesar 1 farad jika dengan tegangan 1 volt dapat memuat muatan elektron sebanyak 1 coulombs. Dengan rumus dapat ditulis :
Q = CV …………….(1)
Q = muatan elektron dalam C (coulombs)
C = nilai kapasitansi dalam F (farads)
V = besar tegangan dalam V (volt)
 , atau melalui hukum ketiga Newton dapat dituliskan
, atau melalui hukum ketiga Newton dapat dituliskan




 C pada pusat koordinat dan muatan q2 = 5
C pada pusat koordinat dan muatan q2 = 5  C terletak pada sumbu x positif berjarak 0,3 meter dari pusat koordinat.
C terletak pada sumbu x positif berjarak 0,3 meter dari pusat koordinat. 


 . Bila diketahui kuat medan E, maka jumlah garis gaya d
. Bila diketahui kuat medan E, maka jumlah garis gaya d yang menembus suatu elemen dA tegak lurus pada E adalah :
yang menembus suatu elemen dA tegak lurus pada E adalah : 

 sudut antara dA dengan bidang yang tegak lurus pada E. Bila kuat medan pada elemen seluas dA dan E, maka jumlah garis gaya yang keluar dari seluruh permukaan S adalah :
sudut antara dA dengan bidang yang tegak lurus pada E. Bila kuat medan pada elemen seluas dA dan E, maka jumlah garis gaya yang keluar dari seluruh permukaan S adalah : 




 qi adalah jumlah muatan yang ada di dalam atau dilingkupi oleh permukaan tetutup S. jadi dengan hukum gauss kita dapat menentukan muatan yang ada di dalam permukaan tetutup, bila kita tahu berapa garis gaya yang keluar dari permukaan tetutup tersebut. Contoh 4.
qi adalah jumlah muatan yang ada di dalam atau dilingkupi oleh permukaan tetutup S. jadi dengan hukum gauss kita dapat menentukan muatan yang ada di dalam permukaan tetutup, bila kita tahu berapa garis gaya yang keluar dari permukaan tetutup tersebut. Contoh 4.
 Atau garis gaya banyaknya 20 buah dan arahnya menembus bidang OABC. Arah dA ada pada sumbu z positif sehingga d = dA
Atau garis gaya banyaknya 20 buah dan arahnya menembus bidang OABC. Arah dA ada pada sumbu z positif sehingga d = dA 











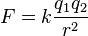

Tidak ada komentar:
Posting Komentar