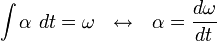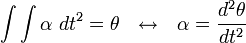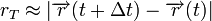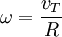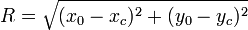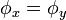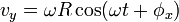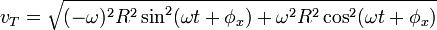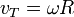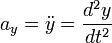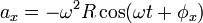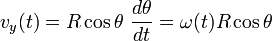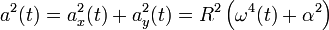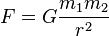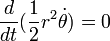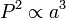PERSAMAAN GERAK
Persamaan gerak adalah suatu fungsi yang memetakan waktu t setiap saat terhadap vektor posisi partikel {x(t),y(t),z(t)} yang dinyatakan dalam aturan
Sistem koordinat adalah suatu metode untuk menentukan letak suatu titik dalam grafik.
kwadran III, dan kwadran IV
 Gambar Koordinat Katesius dan kwadrannya Letak sembarang titik pada bidang dinyatakan dengan pasangan variable berurutan (x,y). Titik P(x,y) berarti bahwa jarak titik P ke sumbu-x dan sumbu-y masing-masing adalah |y| dan |x|. Apabila x <> (atau y <>) maka titik P berada di sebelah kiri (atau sebelah bawah) titik asal O dan apabila x > 0 (atau y > 0) maka titik P terletak di sebelah kanan (atau sebelah atas) titik asal O. Dalam hal ini, x disebut absis titik P sedangkan y disebut ordinat titik P.
Gambar Koordinat Katesius dan kwadrannya Letak sembarang titik pada bidang dinyatakan dengan pasangan variable berurutan (x,y). Titik P(x,y) berarti bahwa jarak titik P ke sumbu-x dan sumbu-y masing-masing adalah |y| dan |x|. Apabila x <> (atau y <>) maka titik P berada di sebelah kiri (atau sebelah bawah) titik asal O dan apabila x > 0 (atau y > 0) maka titik P terletak di sebelah kanan (atau sebelah atas) titik asal O. Dalam hal ini, x disebut absis titik P sedangkan y disebut ordinat titik P. 
Koordinat Kartesian Sistem koordinat kartesian dua dimensi merupakan sistem koordinat yang terdiri dari dua salib sumbu yang saling tegak lurus, biasanya sumbu X dan Y.
Koordinat polar itu formatnya sedikit berbeda yaitu titik=(r,sudut).
- Dimana r adalah jarak dari titik nol ke titik tersebut. kita bisa menghitungnya dengan akar kuadrat dari nilai x dan y.
- Kemudian sudut adalah besar sudut antara garis r tadi dengan sumbu x. kita bisa mendapatkan nilai sudut dengan menghitung arc tan dari nilai y dibagi nilai x
contoh sederhananya begini:
misal ada sebuah titik P yang kalau dalam koordinat cartesian, P ini dituliskan P=(3,4)
maka dalam koordinat polar kita bisa tuliskan P=(5,53)
karena,
r = 5 = akar dari (3 kuadrat + 4 kuadrat)
sudut = 53 derajat (sudut antara garis 0 ke P dengan sumbu x).
Vektor posisi dapat dinyatakan sebagai jumlah vektor dari setiap vektor basis yang sesuai dengan jenis koordinat yang digunakan.
vektor basis adalah vektor yang menjadi vektor dasar/pembentuk/pembangun dari suatu koordinat dan pernyataannya tergentung dari jenis koordinat yang digunakan.
Contoh vektor basis:
vektor basis x, y, z dalam koordinat Cartessian
vektor basis r, theta dalam koordinat lingkaran
vektor basis r, theta, pi dalam koordinat Bola
jadi vektor posisi dapat dituliskan sebagai jumlah dari vektor-vektor basis tersebut.
Contoh penulisan vektor posisi:
S = 2x +3y + 4z (S, x, y, z adalah vektor)
atau bisa juga hanya ditulis (2,3,4)
bentuk ini memiliki aturan urut yaitu (x,y,z)
CONTOH SOAL :
Sebuah partikel B bergerak dengan percepatan a=i+2j. Mula-mula benda diam di titik 2i+4j. Kapan benda memiliki besar perpindahan 5akar2 meter ? (Semua satuan dalam SI).
Jawaban
posisi akhir : r₂(t) = r0 + ½ a t² = r0 + ½ {1,2} t²
posisi awal : r₁(t) = r0
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - (-)
perpindahan: Δr = ½ {1,2} t²
|Δr| = |½ {1,2} t²|
5√2 = √((½ t)² + t²) = ½ t √5
t = 2 √10 detik
padat = 2 √10 detik, perpindahan benda = 5√2 meter.
GERAK TRANSLASI
Gerak lurus adalah gerak suatu obyek yang lintasannya berupa garis lurus. Dapat pula jenis gerak ini disebut sebagai suatu translasi beraturan. Pada rentang waktu yang sama terjadi perpindahan yang besarnya sama.(wikipedia
Gerak lurus dibagi menjadi 2 yaitu
Gerak lurus beraturan (GLB) adalah gerak lurus suatu obyek, dimana dalam gerak ini kecepatannya tetap atau tanpa percepatan, sehingga jarak yang ditempuh dalam gerak lurus beraturan adalah kelajuan kali waktu.
Misal :
- Kereta melaju dengan kecepatan yang sama di jalur rel yang lurus
- Mobil di jalan tol dengan kecepatan tetap stabil di dalam perjalanannya.
 kecepatan sesaat.
kecepatan sesaat.
PERCEPATAN
Setiap benda yang kecepatannya berubah dikatakan mengalami percepatan. Misalnya sebuah mobil atau sepeda motor (sedang bergerak ke arah tertentu) yang kecepatannya berubah dari 0 sampai 70 km/jam berarti dipercepat. Apabila suatu mobil/sepeda motor mengalami perubahan kecepatan seperti ini dalam waktu yang lebih singkat/lebih cepat dari mobil/sepeda motor yang lain, maka dikatakan bahwa mobil tersebut mendapat percepatan yang lebih besar. Jadi percepatan menyatakan seberapa cepat kecepatan sebuah benda berubah.
Percepatan Rata-Rata
Percepatan rata-rata diartikan sebagai perubahan kecepatan dibagi waktu yang diperlukan untuk perubahan tersebut.

Percepatan merupakan besaran vektor, tetapi untuk gerakan satu dimensi, kita hanya perlu menggunakan tanda + dan – untuk menunjukan arah terhadap sistem koordinat yang dipakai.
Percepatan Sesaat
Percepatan sesaat, a, dapat didefinisikan dengan analogi/perbandingan terhadap kecepatan sesaat, untuk suatu saat tertentu.
KELAJUAN
Pada pokok bahasan tentang Besaran Vektor dan Skalar, telah dijelaskan pengertian vektor dan skalar serta perbedaan antara keduanya. Jika anda belum memahami dengan baik dan benar, sebaiknya dipelajari terlebih dahulu.
Istilah laju/kelajuan menyatakan seberapa jauh sebuah benda berjalan/berpindah dalam suatu selang waktu tertentu. Kelajuan merupakan salah satu besaran turunan yang tidak bergantung pada arah, sehingga kelajuan termasuk skalar. Seperti jarak, kelajuan termasuk besaran skalar yang nilainya selalu positif. Alat pengukur kelajuan adalah speedometer, digunakan pada sepeda motor, mobil atau kendaraan lainnya. Anda pasti sering melihat alat tersebut
Kelajuan Rata-rata
Kelajuan/laju rata-rata suatu benda yang bergerak diartikan sebagai jarak total yang ditempuh sepanjang lintasan gerak benda dibagi waktu yang diperlukan untuk menempuh jarak yang tersebut.
![]()
Gerak lurus berubah beraturan (GLBB) adalah gerak lurus suatu obyek, di mana kecepatannya berubah terhadap waktu akibat adanya percepatan yang tetap. Akibat adanya percepatan rumus jarak yang ditempuh tidak lagi linier melainkan kuadratik.
Misal :
- Gerak jatuhnya tetesan air hujan dari atap ke lantai
- Mobil yang bergerak di jalan lurus mulai dari berhenti
vt = v0 + at
t : waktu
v0 : kecepatan awal
a : percepatan
vt : kecepatan pada saat t
x = v0t + ½ at2
x : jarak
v0 : kecepatan awal
t : waktu
a : percepatan
GLBB dibagi menjadi 2 macam :
a. GLBB dipercepat
Adalah GLBB yang kecepatannya makin lama makin cepat, contoh GLBB dipercepat adalah gerak buah jatuh dari pohonnya.
Grafik hubungan antara v terhadap t pada GLBB dipercepat adalah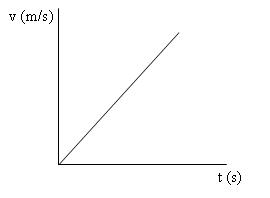
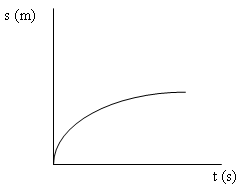
Sedangkan Grafik hubungan antara s terhadap t pada GLBB dipercepat
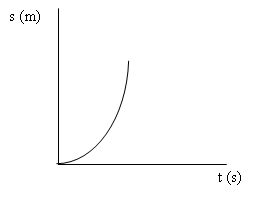
b. GLBB diperlambat
Adalah GLBB yang kecepatannya makin lama makin kecil (lambat). Contoh GLBB diperlambat adalah gerak benda dilempar keatas.
Grafik hubungan antara v terhadap t pada GLBB diperlambat
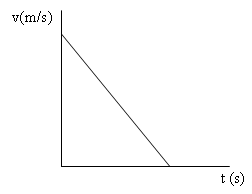
Grafik hubungan antara s terhadap t pada GLBB diperlambat
Gerak Melingkar adalah gerak suatu benda yang membentuk lintasan berupa lingkaran mengelilingi suatu titik tetap. Agar suatu benda dapat bergerak melingkar ia membutuhkan adanya gaya yang selalu membelokkan-nya menuju pusat lintasan lingkaran. Gaya ini dinamakan gaya sentripetal. Suatu gerak melingkar beraturan dapat dikatakan sebagai suatu gerak dipercepat beraturan, mengingat perlu adanya suatu percepatan yang besarnya tetap dengan arah yang berubah, yang selalu mengubah arah gerak benda agar menempuh lintasan berbentuk lingkaran.
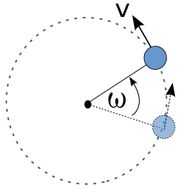
Besaran gerak melingkar
Besaran-besaran yang mendeskripsikan suatu gerak melingkar adalah 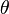 ,
,  dan
dan  atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan
atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan  ,
, 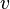 dan
dan  .
.
| Gerak lurus | Gerak melingkar | ||
|---|---|---|---|
| Besaran | Satuan (SI) | Besaran | Satuan (SI) |
poisisi  | m | sudut 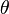 | rad |
kecepatan 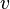 | m/s | kecepatan sudut  | rad/s |
percepatan  | m/s2 | percepatan sudut  | rad/s2 |
| - | - | perioda 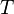 | s |
| - | - | radius  | m |
Turunan dan integral
Seperti halnya kembarannya dalam gerak linier, besaran-besaran gerak melingkar pun memiliki hubungan satu sama lain melalui proses integrasi dan diferensiasi.
Hubungan antar besaran sudut dan tangensial
Antara besaran gerak linier dan melingkar terdapat suatu hubungan melalui  khusus untuk komponen tangensial, yaitu
khusus untuk komponen tangensial, yaitu
Perhatikan bahwa di sini digunakan  yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
untuk suatu selang waktu kecil atau sudut yang sempit.
Jenis gerak melingkar
Gerak melingkar dapat dibedakan menjadi dua jenis, atas keseragaman kecepatan sudutnya  , yaitu:
, yaitu:
- gerak melingkar beraturan, dan
- gerak melingkar berubah beraturan.
Gerak melingkar beraturan
Gerak Melingkar Beraturan (GMB) adalah gerak melingkar dengan besar kecepatan sudut  tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial
tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial 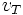 dengan jari-jari lintasan
dengan jari-jari lintasan 
Arah kecepatan linier 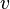 dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial
dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial 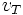 . Tetapnya nilai kecepatan
. Tetapnya nilai kecepatan 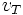 akibat konsekuensi dar tetapnya nilai
akibat konsekuensi dar tetapnya nilai  . Selain itu terdapat pula percepatan radial
. Selain itu terdapat pula percepatan radial  yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
Bila 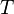 adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran
adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran  , maka dapat pula dituliskan
, maka dapat pula dituliskan
Kinematika gerak melingkar beraturan adalah
dengan  adalah sudut yang dilalui pada suatu saat
adalah sudut yang dilalui pada suatu saat 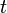 ,
,  adalah sudut mula-mula dan
adalah sudut mula-mula dan  adalah kecepatan sudut (yang tetap nilainya).
adalah kecepatan sudut (yang tetap nilainya).
Gerak melingkar berubah beraturan
Gerak Melingkar Berubah Beraturan (GMBB) adalah gerak melingkar dengan percepatan sudut  tetap. Dalam gerak ini terdapat percepatan tangensial
tetap. Dalam gerak ini terdapat percepatan tangensial  (yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial
(yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial 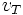 ).
).
Kinematika GMBB adalah
dengan  adalah percepatan sudut yang bernilai tetap dan
adalah percepatan sudut yang bernilai tetap dan  adalah kecepatan sudut mula-mula.
adalah kecepatan sudut mula-mula.
Persamaan parametrik
Gerak melingkar dapat pula dinyatakan dalam persamaan parametrik dengan terlebih dahulu mendefinisikan:
- titik awal gerakan dilakukan
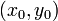
- kecepatan sudut putaran
 (yang berarti suatu GMB)
(yang berarti suatu GMB) - pusat lingkaran

untuk kemudian dibuat persamaannya [2].
Hal pertama yang harus dilakukan adalah menghitung jari-jari lintasan  yang diperoleh melalui:
yang diperoleh melalui:
Setelah diperoleh nilai jari-jari lintasan, persamaan dapat segera dituliskan, yaitu
dengan dua konstanta 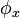 dan
dan 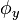 yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai
yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai 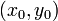 , maka dapat ditentukan nilai
, maka dapat ditentukan nilai 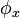 dan
dan 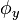 :
:
Perlu diketahui bahwa sebenarnya
karena merupakan sudut awal gerak melingkar.
Hubungan antar besaran linier dan angular
Dengan menggunakan persamaan parametrik, telah dibatasi bahwa besaran linier yang digunakan hanyalah besaran tangensial atau hanya komponen vektor pada arah angular, yang berarti tidak ada komponen vektor dalam arah radial. Dengan batasan ini hubungan antara besaran linier (tangensial) dan angular dapat dengan mudah diturunkan.
Kecepatan tangensial dan kecepatan sudut
Kecepatan linier total dapat diperoleh melalui
dan karena batasan implementasi persamaan parametrik pada gerak melingkar, maka
dengan
diperoleh
sehingga
Percepatan tangensial dan kecepatan sudut
Dengan cara yang sama dengan sebelumnya, percepatan linier total dapat diperoleh melalui
dan karena batasan implementasi persamaan parametrik pada gerak melingkar, maka
dengan
diperoleh
sehingga
Kecepatan sudut tidak tetap
Persamaan parametric dapat pula digunakan apabila gerak melingkar merupakan GMBB, atau bukan lagi GMB dengan terdapatnya kecepatan sudut yang berubah beraturan (atau adanya percepatan sudut). Langkah-langkah yang sama dapat dilakukan, akan tetapi perlu diingat bahwa
dengan  percepatan sudut dan
percepatan sudut dan  kecepatan sudut mula-mula. Penurunan GMBB ini akan menjadi sedikit lebih rumit dibandingkan pada kasus GMB di atas.
kecepatan sudut mula-mula. Penurunan GMBB ini akan menjadi sedikit lebih rumit dibandingkan pada kasus GMB di atas.
Persamaan parametrik di atas, dapat dituliskan dalam bentuk yang lebih umum, yaitu:
di mana  adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara
adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara 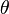 ,
,  dan
dan  melalui proses integrasi dan diferensiasi, maka dalam kasus GMBB hubungan-hubungan tersebut mutlak diperlukan.
melalui proses integrasi dan diferensiasi, maka dalam kasus GMBB hubungan-hubungan tersebut mutlak diperlukan.
Kecepatan sudut
Dengan menggunakan aturan rantai dalam melakukan diferensiasi posisi dari persamaan parametrik terhadap waktu diperoleh
dengan
Dapat dibuktikan bahwa
sama dengan kasus pada GMB.
Percepatan total
Diferensiasi lebih lanjut terhadap waktu pada kecepatan linier memberikan
yang dapat disederhanakan menjadi
Selanjutnya
yang umumnya dituliskan
dengan
yang merupakan percepatan sudut, dan
yang merupakan percepatan sentripetal. Suku sentripetal ini muncul karena benda harus dibelokkan atau kecepatannya harus diubah sehingga bergerak mengikuti lintasan lingkaran.
Gerak berubah beraturan
Gerak melingkar dapat dipandang sebagai gerak berubah beraturan. Bedakan dengan gerak lurus berubah beraturan (GLBB). Konsep kecepatan yang berubah kadang hanya dipahami dalam perubahan besarnya, dalam gerak melingkar beraturan (GMB) besarnya kecepatan adalah tetap, akan tetapi arahnya yang berubah dengan beraturan, bandingkan dengan GLBB yang arahnya tetap akan tetapi besarnya kecepatan yang berubah beraturan.
| Kecepatan | GLBB | GMB |
|---|---|---|
| Besar | berubah | tetap |
| Arah | tetap | berubah |
| 1. | Gaya Gesekan di Bidang Datar Dalam bahasan ini Anda akan dijelaskan penurunan persamaan gaya gesekan yang terjadi di bidang datar. Persamaan tersebut hanya sebatas kualitatif saja, sebab analisa kuantitatif terhadap persoalan gaya gesek di bidang datar akan dijelaskan dalam kegiatan belajar 3. Perhatikan sebuah benda (balok) yang terletak di atas lantai datar berikut ini. | |||||||||||
 | ||||||||||||
| Pada balok bekerja beberapa komponen gaya yang dapat Anda uraikan seperti gambar di bawah ini. Anggap balok didorong oleh gaya F ke kanan. | ||||||||||||
 | ||||||||||||
Bila benda belum bergerak (diam), maka pada benda berlaku hukum I Newton, perhatikan persamaan berikut ini: , Anda dapat uraikan gaya tersebut dalam arah sumbu x dan sumbu y, sehingga menjadi:
pada sumbu x
Pada sumbu y
Untuk benda yang bergerak, berlaku hukum II Newton. Sehingga persamaan di atas tidak berlaku untuk benda yang bergerak. Penurunan persamaannya dapat dirumuskan sebagai berikut:
F - f = ma, pindah ke ruas kanan dan ma ke ruas kiri, maka F - ma = f atau
Pada sumbu y
N - W = 0
| ||||||||||||
| 2. | Gaya Gesekan di Bidang Miring | ||||||||||||
Secara kualitatif persamaan gaya gesekan pada bidang miring dapat diuraikan sebagai berikut. Perhatikan gambar di bawah ini! | |||||||||||||
 | |||||||||||||
Ada dua kemungkinan gerak yang dialami balok di bidang miring tersebut, yaitu: pertama, balok meluncur turun ke bawah dan kedua, balok naik ke atas jika terdapat gaya dorong F yang mendorong balok naik ke atas.
|
Terdapat dua jenis
Gaya gesekan yang bekerja pada dua permukaan benda yang bersentuhan, ketika benda tersebut belum bergerak disebut gaya gesek statik (lambangnya fs). Gaya gesek statis yang maksimum sama dengan gaya terkecil yang dibutuhkan agar benda mulai bergerak. Ketika benda telah bergerak, gaya gesekan antara dua permukaan biasanya berkurang sehingga diperlukan gaya yang lebih kecil agar benda bergerak dengan laju tetap. Ketika benda telah bergerak, gaya gesekan masih bekerja pada permukaan benda yang bersentuhan tersebut. Gaya gesekan yang bekerja ketika benda bergerak disebut gaya gesekan kinetik (lambangnya fk) (kinetik berasal dari bahasa yunani yang berarti “bergerak”). Ketika sebuah benda bergerak pada permukaan benda lain, gaya gesekan bekerja berlawanan arah terhadap kecepatan benda. Hasil eksperimen menunjukkan bahwa pada permukaan benda yang kering tanpa pelumas, besar gaya gesekan sebanding dengan Gaya Normal.
KOOFISIEN GESEKAN STATIK DAN KINETIK


Perhatikan bahwa hubungan antara gaya normal dan gaya gesekan pada persamaan di atas hanya untuk besarnya saja. Arah kedua gaya tersebut selalu saling tegak lurus satu dengan yang lain, sebagaimana diperlihatkan pada gambar di bawah ini. Berikut ini keterangan untuk gambar di bawah : fk adalah gaya gesekan kinetik, fs adalah gaya gesekan statik, F adalah gaya tarik, N adalah gaya normal, w adalah gaya berat, m adalah massa, g adalah percepatan gravitasi.


Contoh Soal 1 :
Sebuah buku berada dalam keadaam diam di atas meja yang permukaannya datar. Koofisien gesekan statik adalah 0,4 dan koofisien gesekan kinetik adalah 0,30. Jika massa buku tersebut adalah 1 kg, berapakah Gaya minimum yang diberikan agar buku itu mulai bergerak ? anggap saja percepatan gravitasi (g) = 10 m/s2

Panduan Jawaban :
Terlebih dahulu kita hitung besar Gaya Normal (N).
N = w = m g = (1 kg) (10 m/s2) = 10 kg m/s2 = 10 N.
Setelah memperoleh besar Gaya Normal, selanjutnya kita hitung besar gaya gesek statis (fs).
![]()
Besar gaya gesek statis adalah 4 N. Agar buku dapat bergerak, maka gaya tarik minimum yang diberikan harus lebih besar dari 4 Newton (agar benda mulai bergerak maka F > fs)
Contoh Soal 2 :
Sebuah balok bermassa 10 kg diletakkan pada bidang miring sebagaimana tampak pada gambar di bawah. Jika sudut yang dibentuk antara bidang miring dengan permukaan lantai sebesar 30o dan koofisien gesekan kinetik adalah 0,4, berapakah gaya gesekan kinetis yang bekerja pada permukaan balok dan bidang miring ?

Panduan Jawaban

Gravitasi adalah gaya tarik-menarik yang terjadi antara semua partikel yang mempunyai massa di alam semesta. Fisika modern mendeskripsikan gravitasi menggunakan Teori Relativitas Umum dari Einstein, namun hukum gravitasi universal Newton yang lebih sederhana merupakan hampiran yang cukup akurat dalam kebanyakan kasus.
Sebagai contoh, Bumi yang memiliki
Setiap
- F adalah besar dari gaya gravitasi antara kedua massa titik tersebut
- G adalah konstanta gravitasi
- m1 adalah besar massa titik pertama
- m2 adalah besar massa titik kedua
- r adalah jarak antara kedua massa titik
Dalam sistem Internasional, F diukur dalam newton (N), m1 dan m2 dalam kilograms (kg), r dalam meter (m), dsn konstanta G kira-kira sama dengan 6,67 × 10−11 N m2 kg−2.
Dari persamaan ini dapat diturunkan persamaan untuk menghitung Berat. Berat suatu benda adalah hasil kali massa benda tersebut dengan percepatan gravitasi bumi. Persamaan tersebut dapat dituliskan sebagai berikut: W = mg. W adalah gaya berat benda tersebut, m adalah massa dan g adalah percepatan gravitasi. Percepatan gravitasi ini berbeda-beda dari satu tempat ke tempat lain.
HUKUM
HUKUM NEWTON I
HUKUM NEWTON I disebut juga hukum kelembaman (Inersia).
Sifat lembam benda adalah sifat mempertahankan keadaannya, yaitu keadaan tetap diam atau keaduan tetap bergerak beraturan.
DEFINISI HUKUM NEWTON I :
Setiap benda akan tetap bergerak lurus beraturan atau tetap dalam keadaan diam jika tidak ada resultan
gaya (F) yang bekerja pada benda itu, jadi:
S F = 0 a = 0 karena v=0 (diam), atau v= konstan (GLB)
HUKUM NEWTON II
a = F/m
S F = m a
S F = jumlah gaya-gaya pada benda
m = massa benda
a = percepatan benda
Rumus ini sangat penting karena pada hampir semna persoalan gerak {mendatar/translasi (GLBB) dan melingkar (GMB/GMBB)} yang berhubungan dengan percepatan den massa benda dapat diselesaikan dengan rumus tersebut.
HUKUM NEWTON III
DEFINISI HUKUM NEWTON III:
Jika suatu benda mengerjakan gaya pada benda kedua maka benda kedua tersebut mengerjakan juga gaya pada benda pertama, yang besar gayanya = gaya yang diterima tetapi berlawanan arah. Perlu diperhatikan bahwa kedua gaya tersebut harus bekerja pada dua benda yang berlainan.
F aksi = - F reaksiHUKUM KEPLER
Hukum Pertama
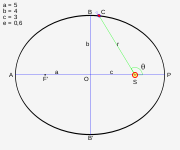
- "Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya."
Pada zaman Kepler, klaim diatas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.
Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproximasi lingkaran. Jadi, kalau ditilik dari observasi jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips. Namun, dari bukti perhitungan Kepler, orbit orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh Pluto, yang diobservasi pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elipse dan kecil ukurannya.
Hukum Kedua
- "Luas daerah yang disapu pada selang waktu yang sama akan selalu sama."
Secara matematis:
dimana 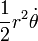 adalah "areal velocity".
adalah "areal velocity".
Hukum Ketiga
Planet yang terletak jauh dari matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepelr ketiga menjabarkan hal tersebut secara kuantitativ.
- "Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari."
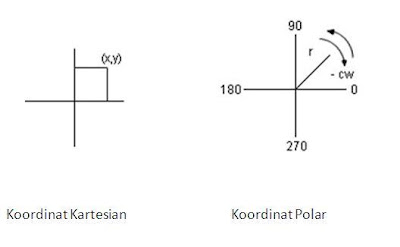
Secara matematis:
dimana P adalah period orbit planet dan a adalah axis semimajor orbitnya.
Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar matahari.